Forward Propogation in CNNs
CNN
Convolutional Neural Networks. That's a mouthful isn't it? People use them all the time, yet they are a total black box. Using Tensorflow, Pytorch or another machine learning module to implement a CNN is interesting, but learning the details can give deeper insights.Simply put,
They are neural networks that take in 2 dimensional inputs, mainly images. They have a variety of applications ranging from face recognition in your smartphone to categorizing tumours as malignant or benign. Recently, CNNs have even outperformed doctors in image recognition.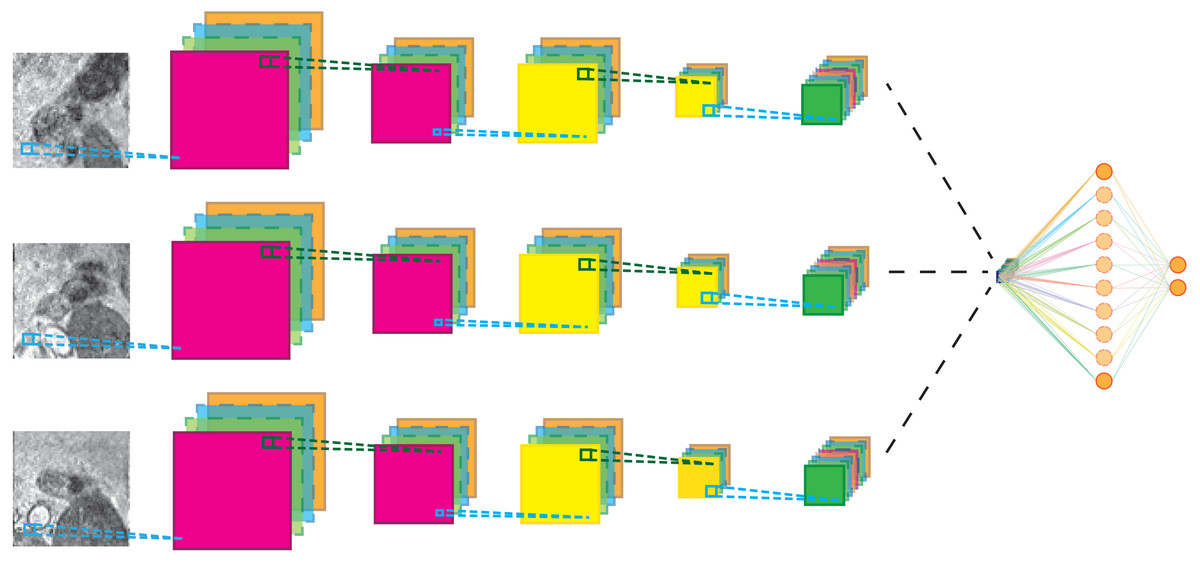
It all starts at Image Processing
Images can be treated as two dimensional inputs. When we are dealing with grayscale images at least. So, if we have a grayscale image, we can directly convert it into a n x m matrix using the pixel values(either 0 or 1) where n is the number of rows and m is the number of columns. In other words, the image is ‘n’ high and ‘m’ wide. Image processing is pretty cool.Color
Hey wait..what about colored images? Well, this is where things get messy. You have to have three “channels” as they call it. One for red, one for green, and one for blue. If you’ve ever done CSS styling, when you say ‘background-color: rgb(128,0,128)”, you are changing the background color to purple using three values for red, green, and blue. Same concept with images, except that you have multiple colors on the same image so you have a matrix for each channel.Convolution
Okay..how do we forward propagate these matrices? Let’s start with grayscale images. Say we choose a 5 x 5 image. In order to forward propagate this image, we first use a process called Convolution. Convolving an image involves taking a filter, and running it across the image. What does that mean? Try using the animation below by clicking the "Convolve" button:Image
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
Filter
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
(1,0,1)*(1,1,1) + (1,1,0) * (0,0,0) + (1,1,0)*(1,1,1)
So, every element in the filter multiplied by the corresponding element
in the image. You repeat this process with every shift of the filter and
you have what's called your "feature map". The general formula for
finding the dimensions of the feature map is:
m x m ** n x n ---> (m - n + 1) x (m - n + 1)
where 'm x m' are the image dimensions, 'n x n' are the filter dimensions and ' ** ' represents the convolution operation.
Multiple Channels
When we have an RGB image, we have to use 3 filters, one for each channel.Image
Filter
Result
As you can see, the result of convolving a 3 x 3 x 3 filter on a 5 x 5 x 3 image, is still a 3 x 3 feature map. How? Well, instead of shifting a square around the image like for grayscale images, think about shifting a cubic filter across the 3-D matrix. Now, to get the first square of the result, multiply every matching square and sum them up. So, each square is the sum of 27 products.
Multiple Filters
First of all, why do we need multiple filters? Why can't we just use a single filter? Well, in order to detect a variety of features and to capture the "atmoic" elements of the image in the first layer, we need to use multiple filters.
Image
Filter 1
Filter2
Result
So, each filter produces a single feature map. The yellow feature map is the result of the first filter convolving, and the coral feature map is the result of the second. Wait a minute...this is similar to how each neuron in a neural net produces a single output. Coincidence? Turns out, there are parallels between the architecture of CNNs and NNs. A filter is analogous to a neuron so a layer of filters could be compared to a layer of neurons.